约瑟夫环与魔术

本篇文章将介绍一个魔术，并且将会通过数学与程序来证明魔术的原理，相信我，这绝对是手法简单，效果上乘的魔术。表演如下：

流程回顾

视频中共有两个效果，这里对第一个效果不做过多解释，这是一个简单的mind force，如果你的观众不是预先有着特定的信仰，绝大部分人都会说7，就像你请观众用英文讲一个颜色，大多数人会说blue一样，当然，这可能失败，如果不中，魔术师会以别的方式来做效果。本文关注后面一个效果，为什么看似随机的过程，观众所选的牌最后一定会落在魔术师那里。我们来回顾下整个流程，整个过程还是很乱的，所以请保持头脑的绝对清醒，最好拿一副牌一起来做：

观众选出两张幸运牌a,b。
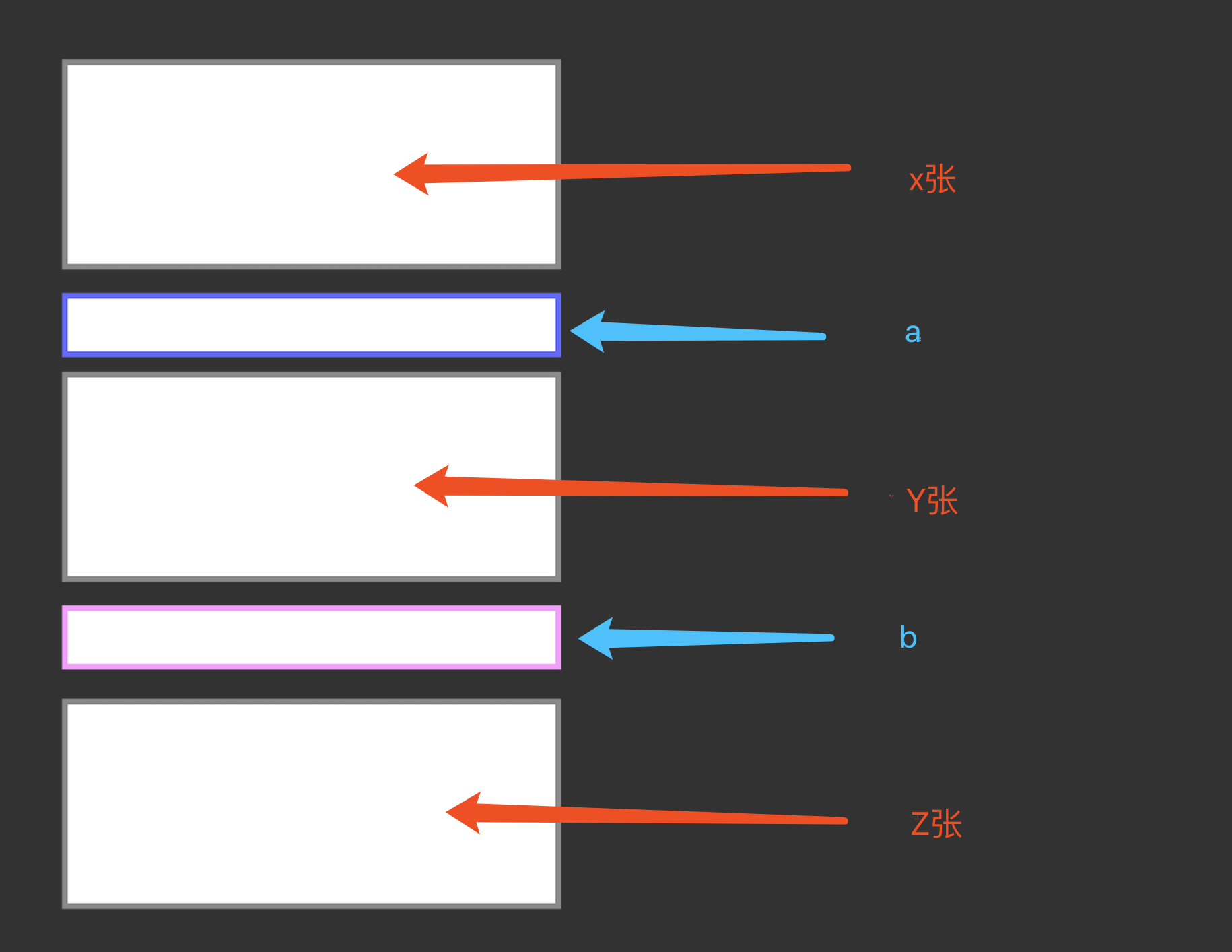
观众说出幸运数字x，魔术师数出x张牌，将a放置x张牌下面，因此a所在的位置为x＋1。
魔术师说出自己幸运数字y，继续数y张牌，将b放置y张牌的底下，因此b所在的位置为x＋1+y＋1
此时，牌被两张幸运牌分成三个区间，分别为x，y，和剩下的区间命名为z。

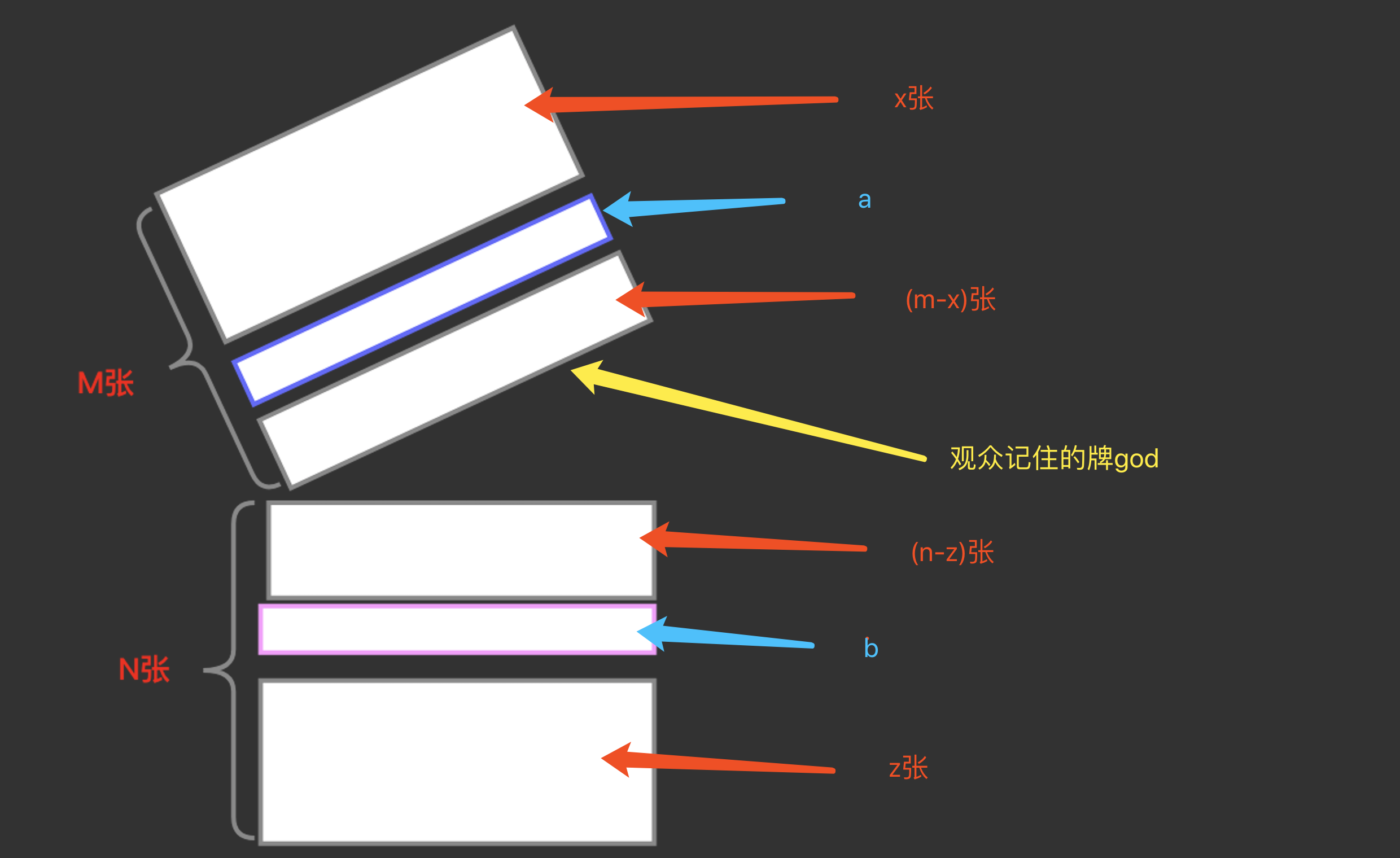
sf1-ttcdn-tos.pstatp.com/obj/ttfe/hzmobile/WechatIMG135_1577007461467.png

魔术师让观众拿起约1/3的牌并观看底牌，说1/3的目的是让观众看到的底牌在y区间，稍后会解释这一目的。我们假设观众所看底牌为god，观众拿起m张。god所在的位置即为m。因此，y区间被god牌分为c、d两个小区间。god在c区间的最后一张，此时有
```
    1）m ＝ x ＋ c
    2）y ＝ c ＋ d
```

魔术师让观众继续拿起剩下牌的1/2，此时的目的是让观众拿到z区间的牌。假设此时拿起的牌为n张，因此，z区间被分为e、f两个小区间，有如下等式：
```
    3）z = e + f
    4）n = d + e + f
```

再将上一步的m张牌首先放下，接着将本次的n张牌放下，所以，目前god所在的位置是倒数f张。

此时，牌区间在此被分为三个，即d、e+x、c+f。
注意，此时才是魔术师做了手脚的一步。它将两张幸运牌取出，美其名曰是给观众更多的幸运。还记得幸运牌a、b的位置吗？a应该在x的最后一张，b应该在d的最后一张。此时魔术师将cf与ex做了交换，此时牌组的顺序为：d c f e x：

c的最后一张就是观众所选的god牌，那d ＋ c 是什么呢？根据公式2）可知，它们相加的值就是y，即魔术师的幸运数字，绕了一大圈，观众最终所选牌的位置还是被魔术师所控制。此时，如果没猜错的话，按照观众一张，魔术师一张的分法，god牌就会落在魔术师这里。魔术师所说的幸运数字是29，那么y值应该是29-7=22，对不对呢？

代码验证

我们可以写一个简单js代码来测试一下：

(function(cardTotalNumber) {
    var cardArray = Array.from(Array(cardTotalNumber), (v,k) => k + 1)
    while(true){
        if(cardArray.length === 1){
            console.log("Cool ! Got the last card , origin number is " + cardArray[0] + ".");
            break;
        }else if(cardArray.length === 0){
            console.log("The last card was missed! ");
            break;
        }else{
            cardArray = cardArray.filter((card, arrayIndex) => arrayIndex % 2 === 1);
            cardArray.reverse();
        }
    }
})(52)

运行结果如下：

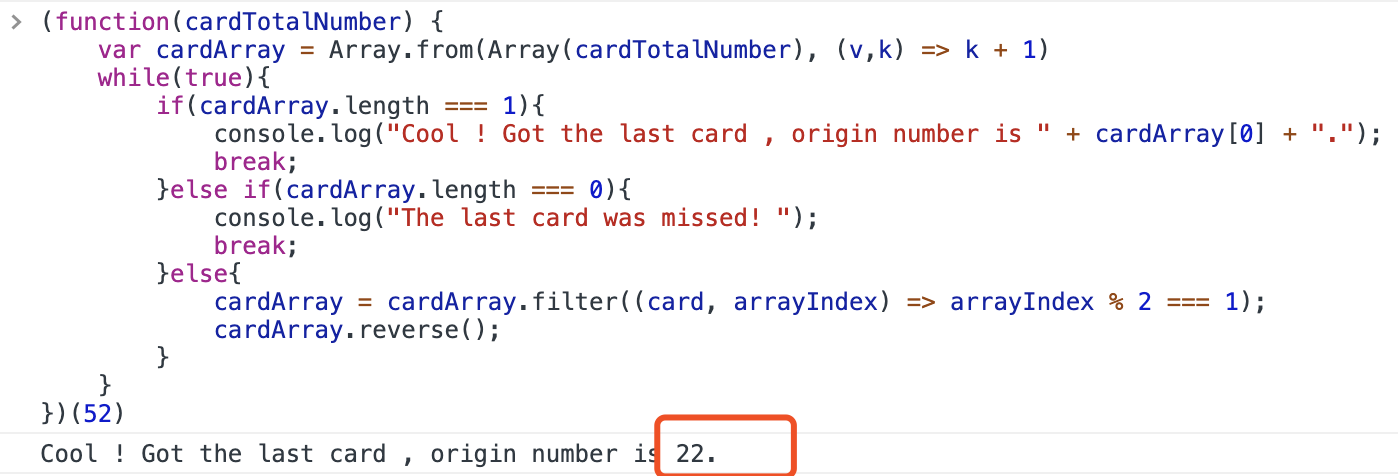
没错，结果是22。

总结

其实，第一次看到这个魔术我最先想到的就是曾经做的算法题，类似于教官让大家报数，报到奇数的就出列，一直重复直到剩下最后一个人，求最后剩下的那个人最开始所报的号码。其实，这类问题大多数都可以归类为约瑟夫环问题，感兴趣的可以搜索一下。

最后，如果你看懂了，恭喜你，可以给朋友好好秀一下，当然，作为一个胸怀大志的programmer，我知道你可能还意犹未尽，那就一鼓作气，试着来挑战下这个吧：

Written by saymagic
on May 14, 2016

← → Top